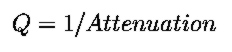
Low frequency events are important observed seismic signals as they indicate the state of the volcanic system. These signals are though to be produced by a resonating fluid trapped within a solid, e.g. a magma filled conduit. To assess the ability of a gas-charged magma to allow resonance, the amount of attenuation or damping a travelling wave experiences due to the magma must be quantified.
Magma is highly viscous and also contains large proportions of gas and crystals, the magma is likely to cause high attenuation making it difficult for any seismic signal to propagate long enough within the conduit to cause resonance.
Previous work on the attenuation of bubbly liquids have assumed that the bubbles change size only by ideal gas expansion, i.e. the bubbles can be considered as `sealed' (Commander and Prosperetti, 1989). It is known that within gas-charged magmas bubbles grow and shrink by the movement of water in and out of the bubbles accompanied by diffusion of the water within the melt. To assess the attenuation of gas-charged magma this `diffusion' mechanism of bubble growth must be included.
Attenuation is quantified through the parameter `Q',
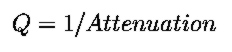
It can be defined through the properties of the material the wave is travelling through, i.e. the viscosities and the elastic modulii (O'Connell and Budiansky, 1978),
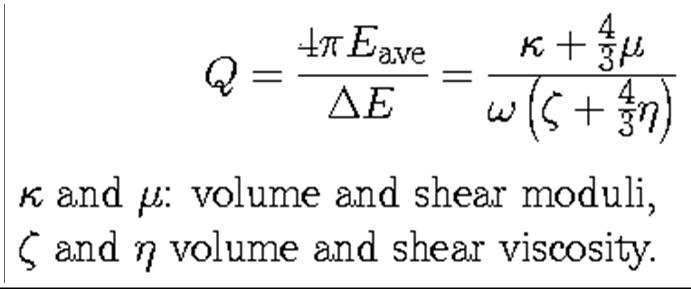
and also through the reaction of the system to the applied stress wave, i.e. the phase lag of the resultant strain with respect to the applied stress (Fig. 1).
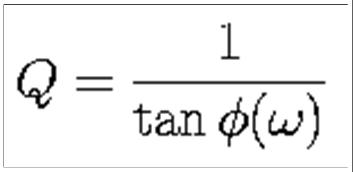
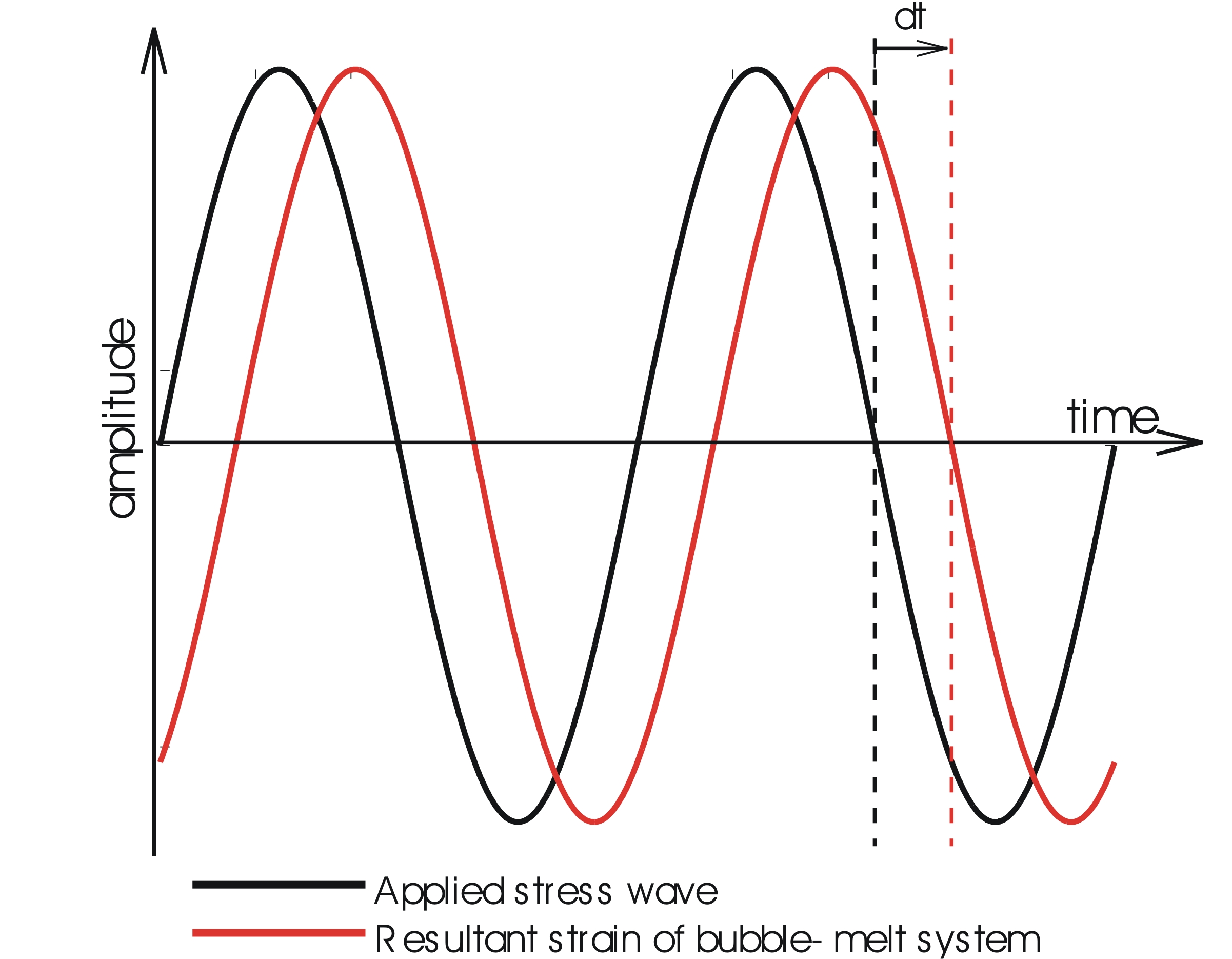
Fig. 1: Variation of the applied stress (black line) and the resultant strain of the system (red line). The time lag measured between the two lines, dt, is then converted into the phase lag and used to determine Q.
By using a numerical bubble growth code we are able to investigate the effects of attenuation including the previously neglected effects of bubble growth by diffusion and mass flux in and out of the bubble (Lyakhovsky et al, 1996). We input the applied stress wave and measure the phase lag of the resultant strain behind the stress, allowing Q to be determined. The level of growth by diffusion and mass flux is increased as the diffusivity, D, is increased. By setting D=0, we effectively `seal' the bubble and stop any mass moving in or out of the bubble, allowing comparisons with previous methods.

Fig. 2: Q against ambient pressure in the magma. As we increase D, Q is decreased implying an increased level of attenuation.
As we increase the amount of growth by diffusion and mass flux the overall level of attenuation is increased, i.e. Q decreased (Fig.2). The movement of water by diffusion within the melt requires energy, therefore this causes attenuation, reducing Q. The observed behaviour of Q with increasing pressure can be explained by the two compteting factors which control attenuation:
1) - As pressure increases the shear viscosity of the melt decreases. This decrease in viscosity causes the level of attenuation to decrease and Q to increase. This behaviour is seen on all lines for low pressures. For D=0, `sealed' bubbles, this is the only factor controlling attenuation, therefore Q increases as pressure increases.
(2) When D>0, we have growth by diffusion and mass flux, so a second factor becomes dominant at high pressures. As the pressure increases, the size of the bubbles decreases. Growth by diffusion and mass flux is inversely proportional to the bubble radius. As the bubbles decrease in size the amount of growth by diffusion and mass flux increases. The more diffusion we have, the more attenuation takes place (see above) and therefore Q decreases. This factor is dominant at the high pressures and causes Q to decrease as pressure increases.
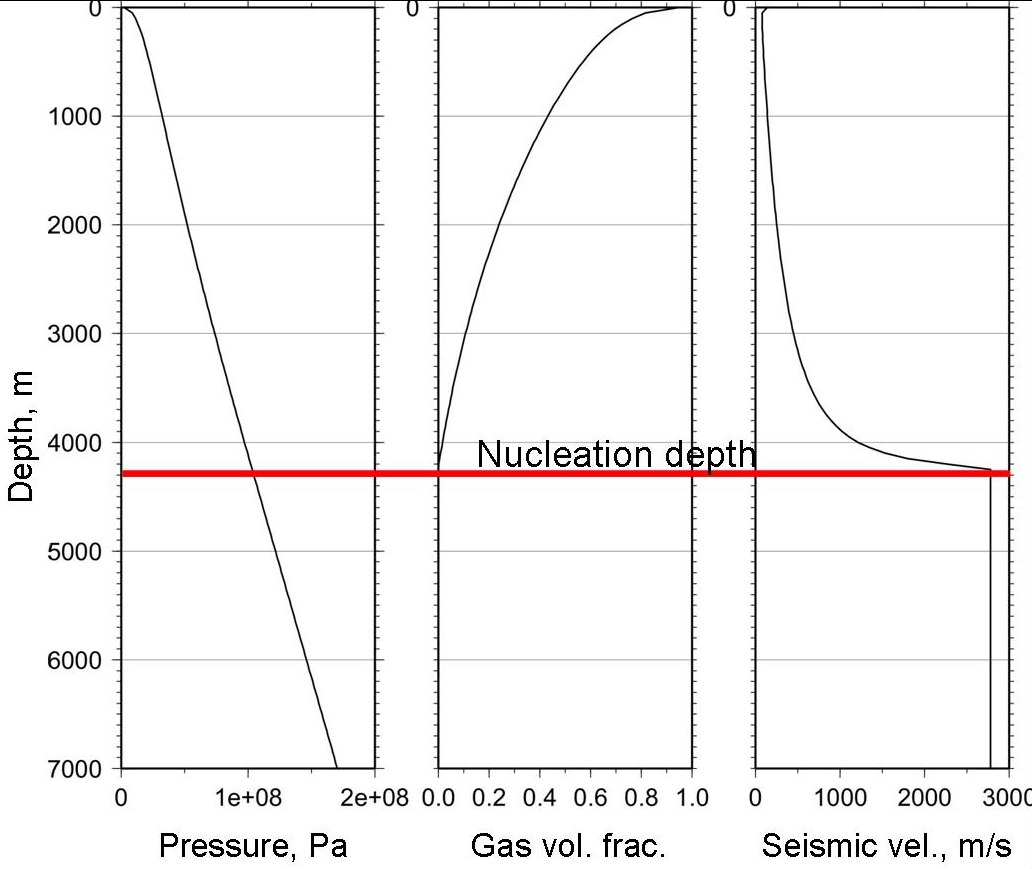
Fig 3: Variation of pressure, gas volume fraction and the seismic velocity with depth in the magma conduit. The nucleation depth is the level at which gas starts to exsolve from the melt forming bubbles.
As we move down the magma conduit, pressure increases and as many magma parameters depend on the pressure, they are also depth dependent (Fig. 3). The seismic velocity is highly dependent on depth, and varies rapidly in the vicinity of the nucleation depth due to the reducing proportion of gas within the magma.
Using this conduit model, Q values were determined for magma within the conduit. Fig. 4 shows Q values assuming no growth by diffusion and no mass flux, D=0 (NO DIFFUSION), and Q including the diffusional growth (WITH DIFFUSION). By including diffusion and mass flux growth we have noticably decreased the range of Q values found within the conduit compared to the `no diffusion' case. This implies the greater attenuation, as discussed above.
The dependence of Q with pressure is noticably changed due to the interaction of the two factors mentioned previously. As a result of the variation of Q with pressure (WITH DIFFUSION), a finite region of high Q values is observed. This identifies a likely region within the magma conduit where Q values are high enough, and attenuation low enough, for seismic waves to sustain resonance. In the vicinity of the nucleation depth, Q decreases rapidly implying large attenuation, perhaps even allowing waves to become fully damped in this region.
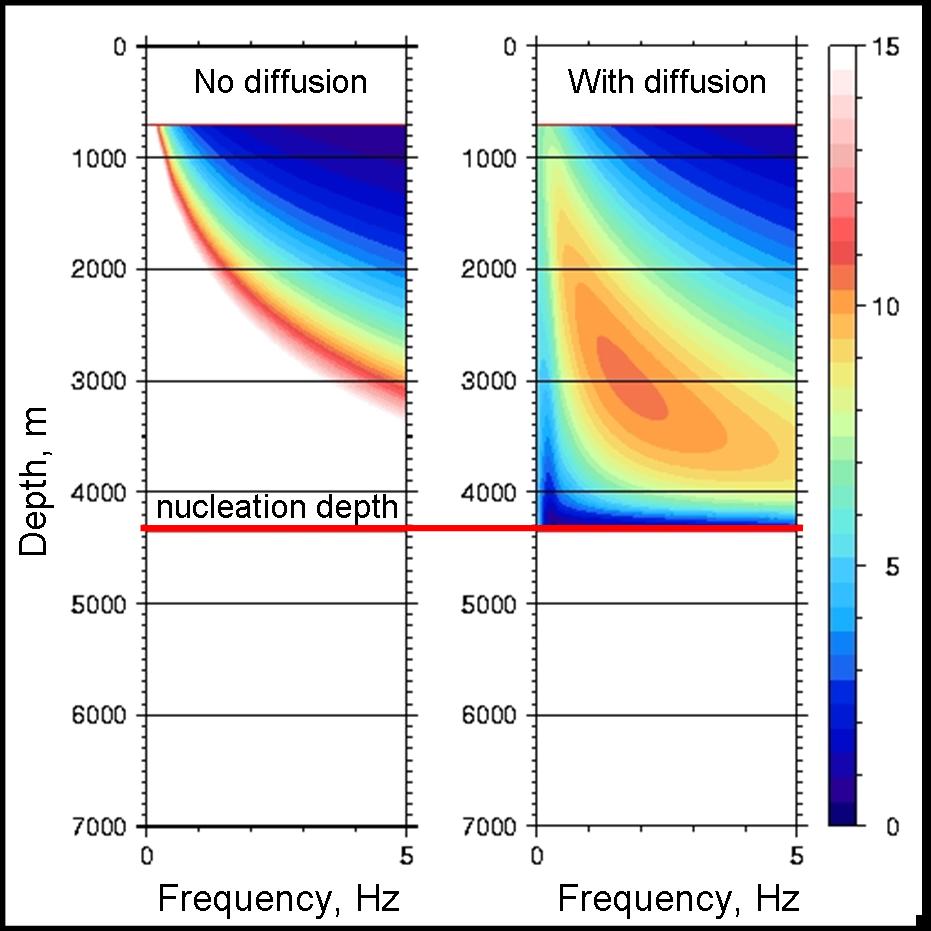
Fig. 4: Variation of Q with depth in the magma conduit and frequency (seismic range). No diffusion: D=0, no mass flux in or out of bubble. With diffusion: including mass flux, D>0.
Fig. 4 also shows that including growth by diffusion and mass flux has altered the Q dependence on frequency. For a sealed bubble, D=0, Q increases as frequency decreases. As frequency -> 0 Q -> infinity (Fig. 4 no diffusion). Whereas when mass flux is included, Q increases as frequency decreases until a maximum Q is reached, then as frequency is further decreased. Q also decreases. This is due to the increased time available for diffusion to occur, causing more attenuation and therefore decreasing Q. However, if we view the very low frequencies, we find that Q decreaces to a minimum as frequency decreases. Then, as frequency -> 0 Q -> infinity (Fig. 5). At very low frequencies the bubble-melt system will be close to equilibrium and therefore will remain in phase with the applied pressure wave and Q = infinity.

Fig. 5: Variation of Q with depth in the magma conduit and frequency. Frequency is plotted on a log10 scale.
In conclusion, the Q values determined in this research imply that attenuation can not be neglected in future studies. By including the previously neglected growth by diffusion and mass flux we have noticably decreased the overall Q values and changed the dependence of Q on frequency and pressure. The Q results within the magma conduit indicate strong damping of waves in the vicinity of the nucleation depth, and a finite maximum Q region where Q values are high enough to allow resonance to be sustained. However, further work must be done, using finite difference methods, to determine whether a seismic wave can propagate within such a magma conduit, and be able to produce resonance (Jousset et al., 2004).
REFERENCES:
Commander and Prosperetti, 1989. Linear pressure waves in bubbly liquids: comparison between theory and experiments. J. Acoust. Soc. Am. Vol.85 No.2 (732-746)
O'Connell and Budiansk, 1978. Measures of dissipation in viscoelastic media. Geophys. Res. Let. Vol.5 No.1 (5-8)
Lyakhovsky, Hurwitz and Navon, 1996. Bubble growth in rhyolitic melts: experimental and numerical investigation. Bull. Volcanology Vol.58 (19-32)
Jousset, Neuberg and Jolly, 2004. Modelling low-frequency volcanic earthquakes in a vicoelastic medium with topography Geophysical Journal International, In press