Broad-band seismological observations from various volcanoes world-wide reveal a wide variety of low-frequency signals. They have been explained with the existence of very slow wave propagating along crack boundary. Chouet (1986) modelled numerically the 'crack wave' characteristics, using a finite difference scheme. Ferrazini and Aki (1987) studied analytically the normal modes trapped in a liquid layer sandwiched between two solid half spaces and gave an analytical expression of the slow wave, which exists for all wavelength.

We model the seismic wave propagation in and around a magma filled conduit embedded in a surrounding medium. We use 2D finite difference staggered grid stress-velocity formulation (Virieux, 1986) expressed at the 4th-order (Levander, 1988) to model major features of low-frequency seismic signatures and compare them with the observations (Neuberg et al., 1998).

In collaboration with the Department of Applied Mathematics of the University of Leeds, the FD code is being further developed including  more sophisticated damping boundary conditions, taper mechanisms and explicit boundary conditions on the conduit walls.
 
 
 
 

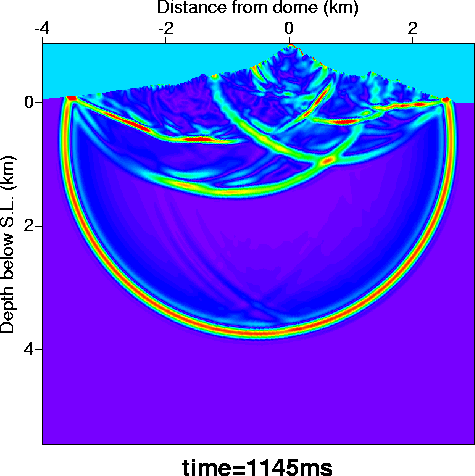Our latest codes compute the seismic wave propagation in and around a magma filled conduit embedded in a viscoelastic medium with topography (Hestholm, 1999). The effect of the topography scattering on the wavefield is represented on the pic on the left (1.124 s after the explosion), for an explosion triggered in a homogeneous medium. The topography is the profile of Monterrat volcano.

Spectrograms calculated from broad band volcano-seismic data shows resonance frequency variation with time. We believe that these variations are related to change of the propagation properties as magma evolves conditions change. Our group models the change in magma properties with time as explained in the page focussing on modelling magma behavior. Accordingly, we introduced a time dependence in our finite difference code. Hence, our synthetic long-period seismograms take into account the magma properties changing with time. Our current work is to compare the synthetic wavefield  with observations of Soufriere Hills volcano, Montserrat. This time dependence provides some clues for the feed-back system in the tremor signal observed in the volcanic Broadband seismic data.

As soon as the critical angle interface waves are generated at the conduit walls provide  seismic energy  through the conduit walls and forming the seismic wave field which is observed at the surface as a low-frequency event.
 
 

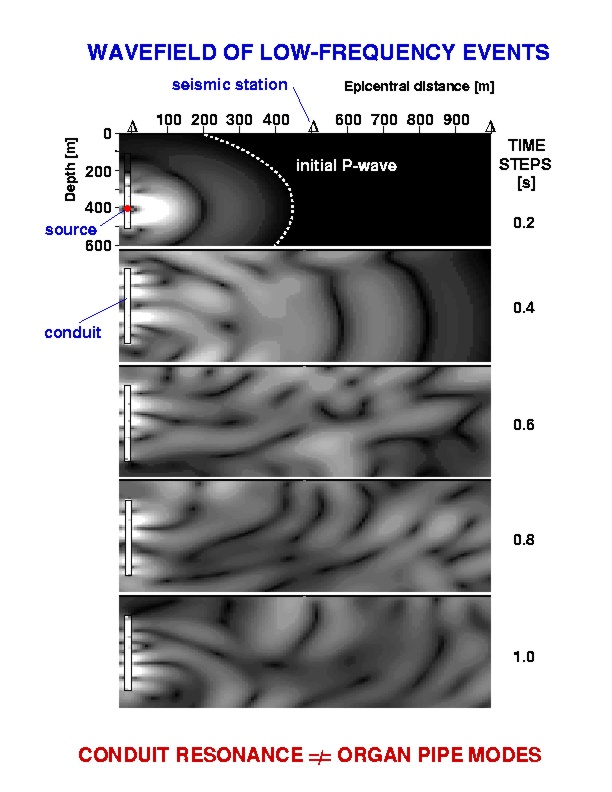Snapshots of  the seismic wave field around a magma filled conduit embedded in an elastic half space. The initial P-wave (dotted line) is the only spherical wave which escapes the conduit; it can be used to locate the actual trigger mechanism of the conduit resonance which forms immediately in and around the conduit. Note that the conduit resonance is fundamentally different from standing waves in the conduit. Standing waves would follow the acoustic velocity of the gas-magma mixture, leading to oversized dimensions of conduit or dykes. The  conduit resonance is formed by interface waves which are dispersive and, depending on the magma parameters and conduit geometry,  very much slower than corresponding standing waves.

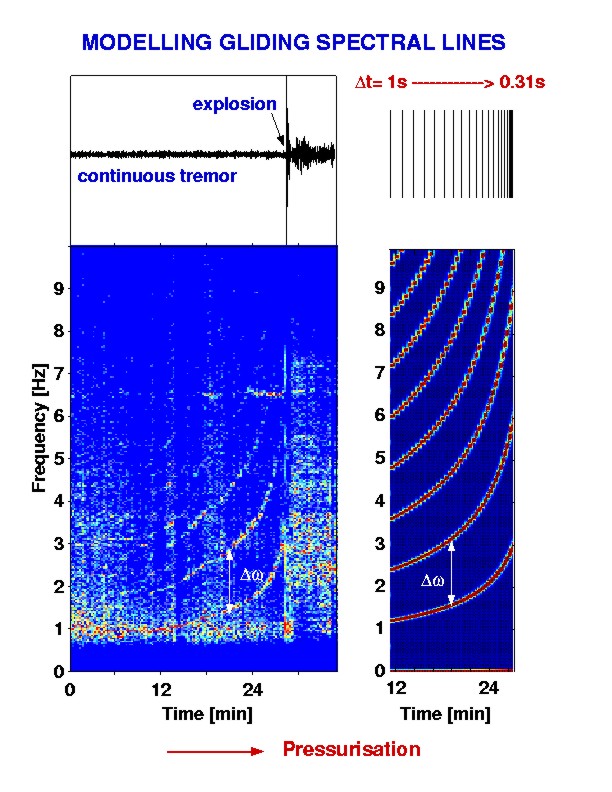Gliding spectral lines as observed on Montserrat and many other volcanoes, can be modelled by repeated triggering of an identical seismic event. The top right 'barcode' indicates the triggering intervals. In our ongoing research we link the change of such a triggering mechanism to changes in the gas-charged magma, mainly to changes in gas volume fraction and pressure. Pressure changes govern the seismic velocity of the magma, and therefore, the  wave field of the conduit resonance.

References:

Chouet B., 1986. Dynamics of a fluid-driven crack in three dimensions by the finite difference method. J. Geophys. Res., 91, 13967-13992

Ferrazini and Aki, 1987. Slow waves trapped in fluid-filled infinite-crack: implication for volcanic tremor. J. Geophys. Res., 92, B9, 9215-9223.

Hestholm, 1999. 2D finite-difference viscoelastic wave modelling including surface topography, Geophysical Prospecting, 2000, 48, 341-373.

Levander, 1988. Fourth-order finite-difference P-SV seismograms, Geophysics, 53, 1425-1436.

Neuberg, J., Baptie, B., Luckett, R. and R. Stewart, 1998, Results from the broad-band seismic network on Montserrat, Geophys. Res. Lett., 25, 19:3661-3664

Virieux, 1986. P-SV wave-propagation in heterogeneous media: velocity-stress finite-difference method, Geophysics, 51, 889-901.