Paddy Smith and Jurgen Neuberg.
Low-frequency events are considered a key part of volcanic monitoring, as they are one of the few tools available that can link surface observations directly to internal volcanic processes and properties. Our model for their generation on Soufrière Hills Volcano, Montserrat, is brittle fracturing of the magma at the conduit walls, providing the seismic trigger mechanism, followed by conduit resonance. The attenuation of seismic waves in a viscous magma is highly dependent on the properties of the attenuating material, in particular the viscous friction, controlled by the melt viscosity, gas content and diffusivity. Therefore by analysis of the seismicity, specifically the coda part of the low-frequency events, we can gain information and constraints on these magma properties.
Our first assertion is that the apparent attenuation of the coda of the recorded seismic signals should be considered a combination of effects from the intrinsic attenuation of the magma and the radiative energy loss of the resonating system.
Decomposing the amplitude loss
Fig 1. Schematic cartoon illustrating how the total amplitude decay of the recorded signal is composed of an intrinsic and radiative part.(Equation: Aki et al. 1977)
First a forward modelling approach is employed, using a two-dimensional finite-difference model to explore the radiative effect on the amplitude decay for a variety of fluid-filled containers, with constraints placed on the geometry by examining the frequencies of the resonance and by using examples from previous studies of the conduit system of Soufrière Hills Volcano, Montserrat.
This allows us to explore the effects of variables such as the conduit geometry, elastic parameter contrast between fluid and solid and source-receiver geometry on the radiative aspect of the attenuation.
Fig 2. Output from finite-difference model illustrating the depth-dependence of the frequency content. At each depth level, the spectrum of a synthetic seismogram is plotted, clearly illustrating a resonance, with a fundamental and harmonic overtones, due to interface waves at the conduit walls.

The intrinsic Q is dependent on the properties of the magma
Fig 4. Results of apparent Q of the synthetic signals from varying the intrinsic Q inside the conduit (for a fixed geometry and parameter contrast and hence, fixed radiative Q). Two regimes are identifiable: 1. Where the apparent Q is greater than the intrinsic Q and resonance dominates and 2. Where the apparent Q is less than the intrinsic Q and radiative energy loss dominates. These two regimes highlight the competing effects of energy trapping due to the resonance and dissipation of the energy due to radiative losses.
This section contains some of the most recent work on applying what we have learnt from the modelling work to a dataset. We chose a set of events from June 1997, an impressive dataset containing several swarms of hundreds of low-frequency events over a 6 day period preceding and following a major dome collapse at Soufrière Hills Volcano.

Fig 5. Families of low-frequency events classified by similar waveforms (Green & Neuberg 2006). Family 'A' is the dominant family before the dome collapse, which occurred at around 12:45pm local time on the 25th June 1997(dashed red line). Due to the large number of events (~3000) and largest amplitudes, family 'A' events were chosen as the first target for investigation and obtaining apparent Q values.
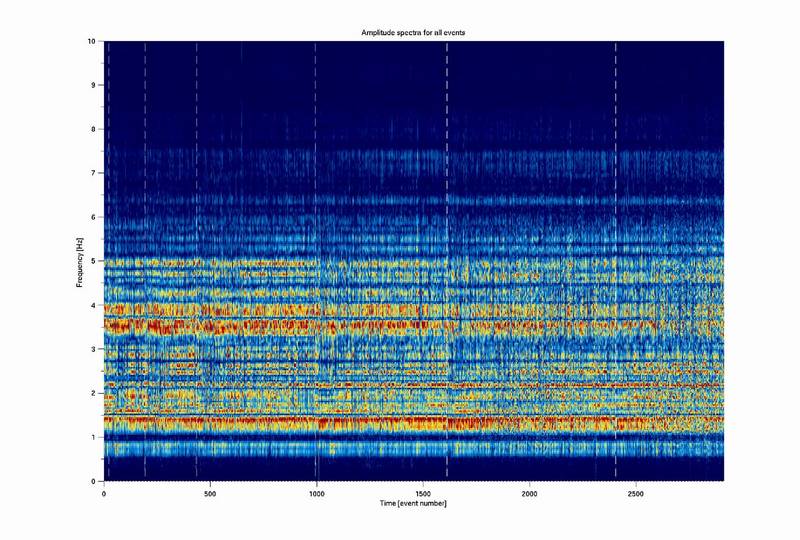
Fig 6. Amplitude spectra for all family 'A' events preceding the dome collapse, shown in temporal order. The dashed lines represent the swarm boundaries ( see Fig 5.). The events have been first band-pass filtered between 0.5 and 5Hz. The events show remarkable consistency of spectral peaks across both individual swarms and across the whole period of several days. This indicates that the they are caused by a common resonating source body that remains stable, in terms of both geometry and magma properties, throughout the whole time period.
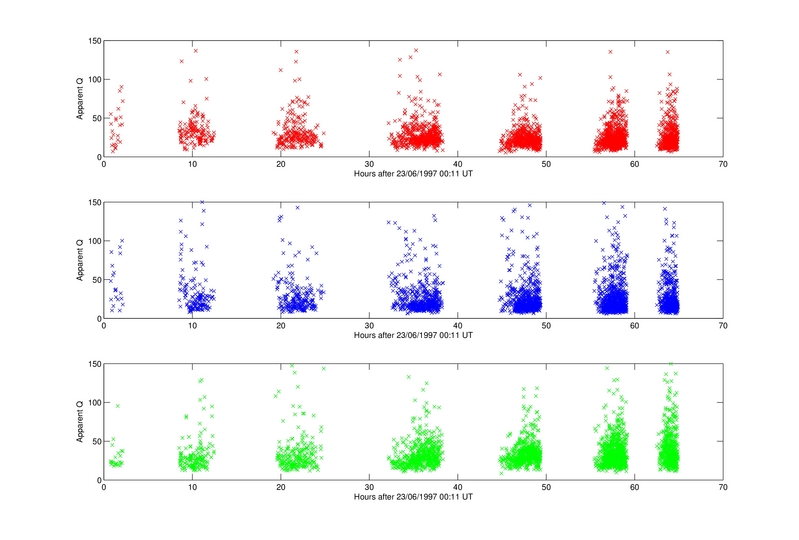
Fig 7. Apparent Q values for each of the three frequency bands chosen from the spectra. The analysis shows each of the seven individual swarms preceding the dome collapse on the 25th June. It is interesting to note an increasing spread of values in each swarm as time progresses.
Green, D. and J. Neuberg, 2006.
Waveform classification of volcanic low-frequency swarms and its implication. J. Volcanol. Geotherm.
Res.,153, 51-63. doi:10.1016/j.jvolgeores.2005.08.003
Jousset P. ,
Neuberg J. and A.D Jolly .
Modelling low-frequency volcanic earthquakes in a viscoelastic medium with
topography. Geophys. J.Int., 159, 776-802.
Aki, K., Fehler, M. and Das, S., 1977.Source mechanism of volcanic tremor: fluid-driven crack models and their application to the 1963 Kilauea Eruption, J. Volcanol. Geotherm. Res., 2, 259-287.